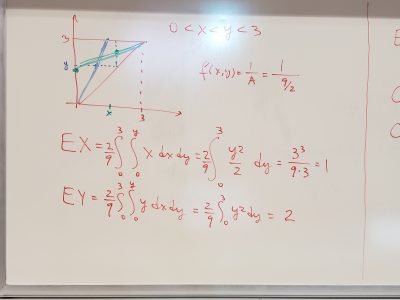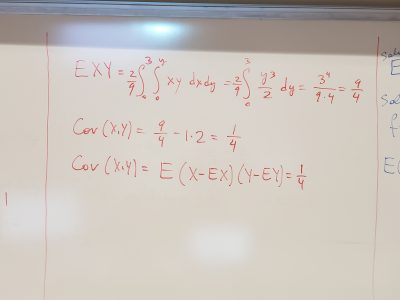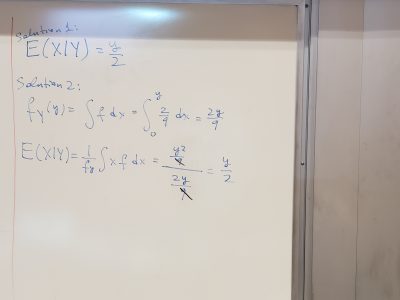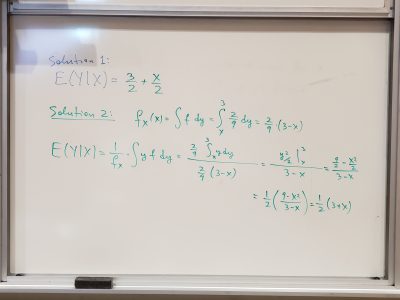In-class question: Suppose we toss a coin 100 times. Use the Central Limit Theorem to approximate the probability to have either at least 55 heads or at most 40 heads.

Additional take-home question: Suppose S is the sum of 48 geometric random variables with p=1/4. Find E(S), Var(S), and the probability P(|S-200|>12). Use the normal table to obtain the numerical answer with accuracy up to three decimal places.

Instruction: write solutions without continuity correction. Extra credit: you will receive extra points for additional solutions with continuity correction.

  

Speaker: John Dever (Gatech)
Time: Tuesday, October 10, 2018 at 8:30 am
Place: MONT 214
Title: Local space and time scaling exponents for diffusion on a compact metric space.

Abstract:
In this talk we define and investigate a local space scaling exponent \(\alpha\) and a local time scaling exponent \(\beta.\)
The exponent \(\alpha\) is the local Hausdorff dimension. We provide several examples of spaces with continuously variable \(\alpha.\) We also investigate a local Hausdorff measure and establish uniqueness up to a strong equivalence of measures satisfying the Ahlfors regularity property \(\mu(B_r(x)) \asymp r^{\alpha(x)}.\)
The exponent \(\beta\) is roughly defined as a critical exponent of the expected number of steps needed for a discrete time random walk on an approximation of the space at scale \(\epsilon\) to leave a ball multiplied by a power \(\epsilon^\beta\) as the scale \(\epsilon\) goes to \(0.\) This exponent can then be localized. Next, we use \(\beta\) to re-normalize the time scale by introducing local exponential waiting times with mean at site \(x\) of [/latex]\epsilon^{\beta(x)}.[/latex] This gives a continuous time walk. We then examine the exit time regularity condition that if \(\mathscr{T}(B)\) is the supremum of the exit times from a ball \(B\) then \(\mathscr{T}(B_r(x))\asymp r^{\beta(x)}.\)
We show that this condition has a number of useful consequences, one of which is a Faber-Krahn type inequality \(\lambda_{1,\epsilon}(B)\geq \frac{c}{R^{\beta(x_0)}}\) where \(B=B_R(x_0)\), \(\lambda_{1,\epsilon}(B)\) is the bottom of the spectrum of the generator of the time-renormalized walk killed outside of \(B\) at stage \(\epsilon\) and \(c\) is a constant independent of \(\epsilon, x_0,\) and \(R.\) Lastly, we investigate convergence of approximating forms using \(\Gamma-\)convergence techniques.