Section 007
Math 3160 — Probability (Revised Syllabus Spring 2020)
Catalog description: Introduction to the theory of probability. Sets and counting, probability axioms, conditional probabilities, random variables, limit theorems. Three credits. Prerequisite: MATH 2110Q, 2130Q or 2143Q.
Open source educational materials are provided (no textbook is necessary for this course)
Standard syllabus for Math 3160 Probability:
- Combinatorics: product rule and permutations; combinations.
- Axioms of Probability: sample spaces, events and set operations; probability axioms.
- Conditional Probability and Independence: conditional probability and Bayes rule; probability trees; independent events.
- Discrete Random Variables: probability mass function (PMF), cumulative distribution function (CDF); expectation; variance, moments, moment generating function (MGF). Uniform, Bernoulli, Binomial, Poisson, Geometric, Hypergeometric distributions; expectation, variance, MGF of these RVs.
- Continuous Univariate Random Variables: probability density function (PDF), CDF, expectation, variance, moments, MGF. Uniform, Exponential, Gamma, Normal distributions; expectation, variance, MGF of these RVs. Transformations (functions) of continuous RVs.
- Jointly Distributed Random Variables: joint PMF/PDF, and CDF; marginal distributions; conditional PMF/PDF; conditional expectation and variance; covariance and correlation coefficients.
- Limit Theorems: Weak Law of Large Numbers, Central Limit Theorem, Normal approximations.
HW 1 (January 20 — January 24):
- read Chapter 1 “Combinatorics”;
- optional: listen to Video Lectures 01a, 01b, 01c;
- do all exercises in this chapter (ask questions in class);
- Sample Quiz 1 for Thursday January 23. solution 1
HW 2 (January 27 — January 31):
- Review HW for week 1 and do any unfinished work;
- read Chapter 2 “The probability set-up”;
- optional: listen to Video Lectures 02a, 02b;
- do all exercises in this chapter (ask questions in class);
- Sample Quiz 2 for Thursday January 30, based on Chapters 1 and 2 solution 2
HW 3 (February 3 — February 7):
- Review HW for week 2 and do any unfinished work;
- read Chapter 3 “Independence” and Chapter 4 “Conditional probability”;
- optional: listen to Video Lecture 3a for Chapter 3 and Video Lectures 3b and 3c for Chapter 4;
- ask questions in class;
- Quiz 3+4 on Thursday, February 6, based on Chapters 3 and 4 (with solution):
- Sample Quiz 3 solution (2019)
- Sample Quiz 4 solution (2019)
- Sample Quiz 3 solution (2018)
- Sample Quiz 4 solution (2018)
- Sample Quiz 3 with solutions (2017)
- Sample Quiz 4 with solutions (2017)
HW 4 (February 10 — February 14):
- Review HW for week 3 and do any unfinished work;
- read Chapter 5 “Random variables”;
- optional: listen to Video Lectures 4a and 4b for Chapter 5;
- ask questions in class;
- Quiz 5 on Thursday, February 13, based on Chapter 5 (with solution):
- Sample Quiz 5 solution (2019)
- Sample Quiz 5 solution (2018)
- Sample Quiz 5 with solutions (2017)
HW 5 (February 17 — February 21):
- Review HW for Chapters 1, 2, 3, 4, 5 and do any unfinished work;
- ask questions in class on Tuesday;
- Test 1 on Thursday February 20, based on Chapters 1, 2, 3, 4, 5.
- You are allowed to bring 1 page of handwritten notes (both sides of an 8 x 11 paper). solution
- Sample Test 1, solution (2019)
- Sample Test 1 with solutions (2018)
- Sample Test 1 with solutions (2017)
- extra problems with solutions
HW 6 (February 24 — February 28):
- read Chapter 6 “Some discrete distributions“;
- optional: listen to Video Lectures 4c and 4d for Chapter 6;
- ask questions in class;
- Quiz 6 on Thursday February 27, based on Chapter 6 (focus on Binomial, Poisson and Geometric distributions). solution
- Sample Quiz 6 with solution (2019)
- Sample Quiz 6 with answers (2018)
- Sample Quiz 6 with solutions (2017)
HW 7 (March 2 — March 6):
- Review HW for the previous week and do any unfinished work;
- read Chapter 7 “Continuous distributions”;
- optional: listen to Video Lectures 5a for Chapter 7;
- ask questions in class;
- Quiz 7 on Thursday March 5, based on Chapter 7. solution
- Sample Quiz 7 with solution (2019)
- Sample Quiz 7 with answers (2018)
- Sample Quiz 7 with solutions (2017)
HW 8 (March 9 — March 13):
- Review HW for the previous week and do any unfinished work;
- read Chapter 8 “Normal distribution” and Chapter 9 “Normal approximation”;
- optional: listen to Video Lecture 5b for Chapters 8 and 9;
- ask questions in class: normal-Gaussian and binomial
- Quiz 8-9 on Thursday March 12, based on Chapters 8 and 9. solution
- Sample Quiz 8-9 with solutions (2019)
- Sample Quiz 8-9 with solutions (2018)
- Sample Quiz 8-9 with solutions (2017)
- graphing applet for the binomial distribution
* Spring Break *
HW 9 (March 23 — March 27)
- Review HW for the previous week and do any unfinished work;
- read Chapter 10 “Some continuous distributions” and do all exercises;
- read and memorize Strategy to transform continuous random variables and this table of continuous distributions;
- optional: listen to Video Lectures 5c and 5d for Chapter 10;
- ask questions via WebEx or email;
- Sample Quiz 10 and solution (2019)
- Sample Quiz 10 and solution (2018)
- Sample Quiz 10 and solutions (2017) with notes
- a sample Test 2a with answers (2017a)
- a sample Test 2b with solutions (2017b) with notes
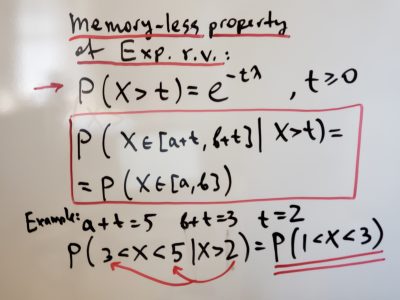
HW 10 (March 30 — April 3)
- Review HW for the previous week and do any unfinished work;
- read Chapter 11 “Multivariate distributions“; do all exercises;
- optional: listen to Video Lectures 6a, 6b, 6c and 6d, for Chapter 11;
- ask questions by email;
- take-home open-book Quiz 11: Thursday April 2, 2pm — Saturday April 4, 9pm. (pass/fail) solution
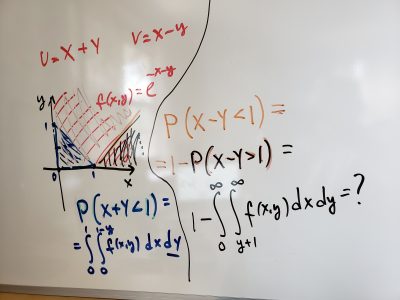
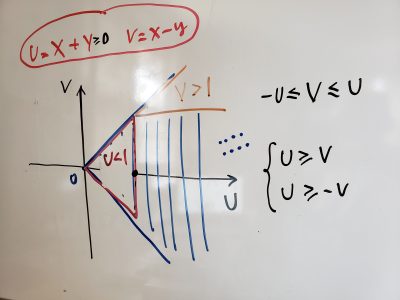
- Sample Quiz 11 and solution (2019)
- Sample Quiz 11 and solution (2018)
HW 11 (April 6 — April 10)
- Review HW for the previous week and do any unfinished work;
- read Chapter 12 “Expectations” and do all examples and exercises;
- optional: listen to Video Lectures 7a, 7b, 7c for Chapter 12;
- ask questions by email (here are pictures from the white board, November 26, 2018 and November 19, 2019);
- take-home open-book Quiz 12: Thursday April 9, 11am — Saturday April 11, 9pm. (pass/fail) solution
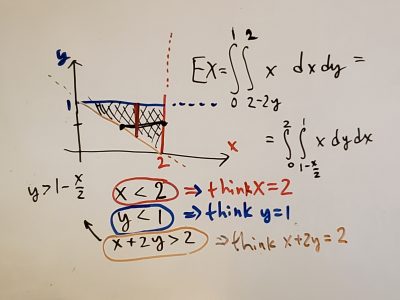
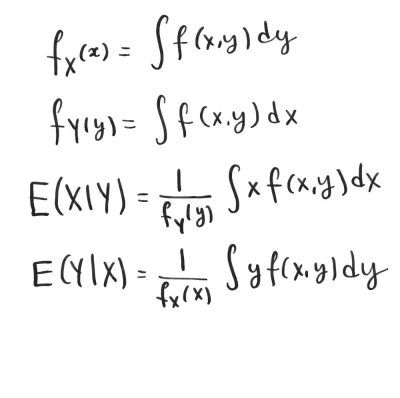
- Sample Quiz 12 and solution (2019)
- Quiz 11-12 with solutions (2017)
- Sample Test 2 with answers (2018)
HW 12 (April 13 — April 17)
- take-home open-book Test 2: Tuesday April 14, 9am — Saturday April 18, 9pm.
- notes
- solution
- mostly based on Chapters 11 and 12 with some questions coming from chapters 1–10
- extra sample Test 2 problems; with answers (2018)
HW 13 (April 20 — April 24)
- Review HW for the previous week and do any unfinished work;
- read Chapter 13 “Moment generating functions” (do all examples and exercises);
- optional: listen to Video Lectures 7d and 7e for Chapter 13;
- take-home open-book Quiz 13: Thursday April 23, 11am — Saturday April 25, 9pm. (pass/fail) notes hints solution
- Sample Quiz 12-13 and answers (2018)
- Sample Quiz 13-14, mostly based on Chapters 13 and 14 with some questions coming from chapters 8, 9, 10, 11, 12. solution (2019)
- Quiz 13-14 with solutions (2017).
- ask questions by email
HW 14 (April 27 — May 1)
- Review HW for the previous week and do any unfinished work;
- read Chapter 14 “Limit laws” (do all examples and exercises);
- optional: listen to Video Lectures 8a and 8b for Chapter 14;
- ask questions by email (here are pictures from the white board, December 5, 2018);
- take-home open-book Quiz 14: Thursday April 30, 11am — Saturday May 2, 9pm. (pass/fail) solution
- Sample Quiz 14, mostly based on Chapter 14 with some questions coming from chapters 8, 9, 10, 11, 12, 13. answers (2018)
- sample final exam problems and answers (2018)
- 9 sample final exam questions with answers (2017)
- 10 sample final exam questions with answers (2017)
Final Exam:
- take-home open-book Final Exam Sunday May 3, 9am — Saturday May 9, 9pm.
Former Final Exam Schedule: 5/8/2020, Friday 3:30pm–5:30pm MONT 321
(all future dates are tentative)